一. 基础知识

根据教材《差错控制编码（原书第二版）》Error Control Coding (Second Edition)，林舒等著，晏坚等译整理。

1. 数字信息的传输与存储

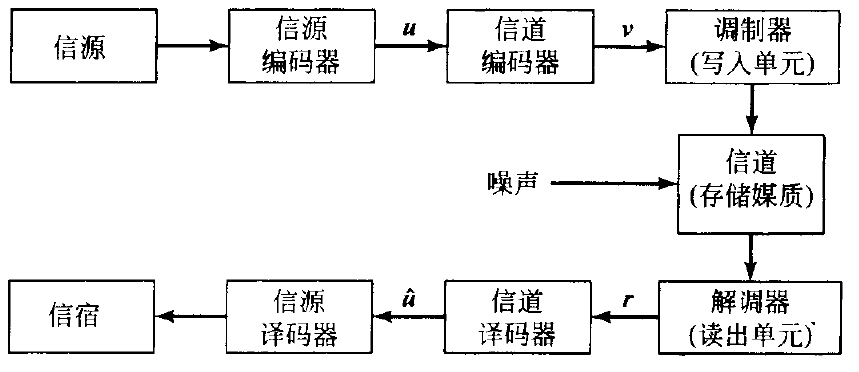
Pasted image 20240305150817|500

信源编码器(Source encoder) 将信源的输出转换为二进制数字（比特）序列，这些序列称为信息序列(information sequence) \boldsymbol{u} 。信源编码不是差错控制编码理论的重点。

信道编码器(channel encoder) 将信息序列 \boldsymbol{u} 变换成离散的编码序列（encoded sequence） \boldsymbol{v} ，称之为码字(codeword) 。

信道译码器(channel decoder) 将接收序列(received sequence) \boldsymbol{r} 变换为二进制序列 \hat{\boldsymbol{u}} ，称为估计信息序列(estimated information sequence)。

2. 码的类型

当前通用的码有两种不同的类型:

分组码(block codes)
卷积码(convolutional codes)

2.1 分组码

分组码编码器把信息序列划分为每组含 k 个信息比特（符号）的消息分组。一个消息分组可用二进制 k 维向量 \boldsymbol{u}=(u_0,u_1,u_2,\cdots,u_{k-1}) 表示，称为一个消息(message) 。在分组编码中，符号 \boldsymbol{u} 用来表示 k 比特消息而不是整个信息序列。总共有 2^k 个可能的不同消息。编码器把每个消息 \boldsymbol{u} 独立地变换成 n 维离散符号向量 \boldsymbol{v}=(v_0,v_1,v_2,\cdots,v_{n-1}) 。同样地，分组码中符号 \boldsymbol{v} 用来表示一个 n 符号组而不是整个编码序列，称之为码字(codeword) 。因此，对应于 2^k 个可能的不同消息，编码器的输出端有 2^k 个可能的不同码字。这 2^k 个长度为 n 的码字的集合称为 (n,k) 分组码(block codes) 。比值R=k/n 称为码率(code rate) ，可解释成每个传送符号所含有的进入编码器的信息比特数。由于 n 符号输出码字只取决于对应的 k 比特输入信息，即每个信息是独立编码的，从而编码器是 无记忆 的。

对二进制码，每个码字 \boldsymbol{v} 也是二进制的。因此，为了使二进制码可用，即对每个消息都能够分配不同的码字，应有 k\leq n 或 R\leq 1 。当 k<n 时，可对每个消息附加 n-k 个冗余比特来构成码字。这些冗余比特将使码具有抵抗信道噪声的能力。对于固定码率 R ，在保持比值 k/n 不变的条件下，可通过增加分组码长度 n 和信息比特数 k 来添加更多的冗余比特。如何选择这些冗余比特，以实现在有噪信道上的可靠信息传输是设计编码器的一个主要问题。

2.2 卷积码

卷积码编码器同样接受 k 比特分组的信息序列 \boldsymbol{u} ，并产生 n 符号组的编码序列 \boldsymbol{v} （卷积码编码器中，符号 \boldsymbol{u} 和 \boldsymbol{v} 用来表示分组的序列而非单个分组）。但是，每一个编码分组不仅取决于当前单位时间对应的 k 比特消息组，而且与前 m 个消息组有关。此时，编码器的存储级数(memory order) 为 m 。编码器所产生的所有可能的输出编码序列的集合构成了一个码。比值R=k/n 称为码率(code rate)。

对于二进制卷积码，当 k<n 或 R<1 时，在信息序列中加入用于抵抗信道干扰的冗余比特。通常 k 和 n 都是较小的整数，当固定 k 和 n 从而码率 R 也被固定时，增大码的存储级数 m 可以增大冗余度。

3. 调制与编码

3.1 BPSK

在通信系统中，对于编码器的每个输出符号，调制器必须选定一个适于传输的、持续时间为 T 秒的波形。在二进制码的情况下，调制器必须产生两个信号中的一个：对应于编码信号“1”的 s_1(t) 或对应于编码信号“0”的 s_2(t) 。对于宽带信道，信号的最优选择是

s_1\left(t\right)=\sqrt{\frac{2E_s}T}{\mathrm{cos}}2\pi f_0t,\quad0\leq t\leq T

s_{2}(t)=\sqrt{\frac{2 E_{s}}{T}} \cos \left(2 \pi f_{0} t+\pi\right)=-\sqrt{\frac{2 E_{s}}{T}} \cos 2 \pi f_{0} t, \quad 0 \leqslant t \leqslant T

其中载波信号频率 f_0 是 1/T 的整数倍，E_s 是每个信号的能量。由于载波 {\mathrm{cos}}2\pi f_0t 的相位随着编码器输出的变化而取 0 或 \pi ，这种调制被称为二进制相移键控 (binary- phase- shift- keying, BPSK)。

3.2 AWGN

一种广泛存在于各种通信系统中的噪声干扰是加性白色高斯噪声(additive white Gaussian noise, AWGN) 。若传输的信号为 s(t)(=s_1(t) 或s_2(t) ），则接收信号为

r(t)=s(t)+n(t)

式中的 n(t) 是一个高斯随机过程，其单边功率谱密度(power spectral density, PSD) 为 N_0 。

3.3 接收信号的输出

在每个 T 秒的间隔上，解调器必须产生一个相应于接收信号的输出。该输出可以是一个实数，或者是预先选定的离散符号集中的一个元素，这取决于解调器的设计。最优解调器通常包含一个匹配滤波器或者香干检测器，后面再有一个采样开关，每隔 T 秒对输出进行采样。对于带相干检测的BPSK调制，其采样输出是一个实数

y=\int_{0}^{T} r(t) \sqrt{\frac{2 E_{s}}{T}} \cos 2 \pi f_{0} t \mathrm{~d} t

未经量化的解调器输出序列可以直接送到信道译码器进行处理。在这种情况下，信道译码器必须能够处理未经量化的输入，也即必须能够处理实数。更为常用的一种译码方法是将实数检测器的输出 y 量化为有限的 Q 个离散输出符号中的一个。在这种情况下，信道译码器为离散输入，即必须能够处理离散值。大多数编码通信系统采用某种形式的离散处理。

3.4 信道建模

如果在给定时间间隔内检测器的输出仅和该间隔内传输的信号有关，而与任何以前传输的信号无关，则称此信道是无记忆(memoryless) 的。在这种情况下，M 进制输入的调制器、物理信道和 Q 进制输出的解调器组合在一起，可以用一个离散无记忆信道(discrete memoryless channel, DMC) 来建模。离散无记忆信道可以用一组转移概率(transition probabilities) P(j\mid i)(0\leq i \leq M-1, 0\leq j \leq Q-1) 来完全描述，其中 i 代表调制器输入的符号， j 代表解调器输出的符号，而 P(j\mid i) 是发送为 i 接收为 j 的概率。

例如，考虑这样一个通信系统：

采用二进制调制（M=2）
噪声的幅度分布是对称的
解调器的输出量化为Q=2 个电平
这种情况下可以得到一个特别简单而实际上极为重要的信道模型，称为二进制对称信道(binary symmetric channel) 。

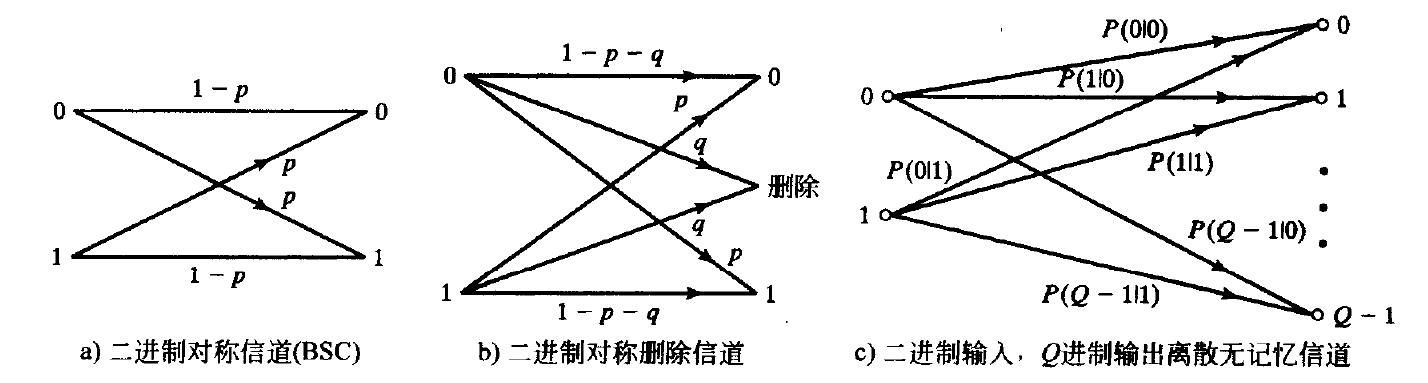
Pasted image 20240305163248|600

转移概率 p 可以由所采用的信号、噪声的概率分布、解调器输出的量化阈值等已知信息来计算。当BPSK调制用于AWGN信道，采用最优相干检测和二进制输出量化时，二进制对称信道的转移概率就是在等概输入信号条件下的非编码BPSK的误比特率，由

p=Q\left(\sqrt{2 E_{s} / N_{0}}\right)

给出，其中Q(x) \triangleq \frac{1}{\sqrt{2 \pi}} \int_{x}^{\infty} \mathrm{e}^{-y^{2 / 2}} \mathrm{~d} y 是高斯统计的互补误差函数，或者简称为Q函数。

解调器的硬判决和软判决

当采用二进制编码时，调制器仅有二进制（M=2）输入。类似地，当解调器的输出采用二进制量化（Q=2）时，译码器也只有二进制输入。在这种情况下，我们称解调器采用硬判决（hard decision） 。当Q>2 （或输出未经过量化）时，我们称解调器采用的是软判决（soft decision） 。在这种情况下，译码器必须接受多电平（或连续信号）的输入，这会增加译码器实现的难度，但是软判决译码较硬判决译码在性能上会有明显的提高。

假设解调器的输入信号是有限离散字符集X=\left\{x_{0}, x_{1}, \cdots, x_{M-1}\right\} 中的符号，解调器的输出未经量化。在此情况下，调制器、物理信道和解调器组成了一个离散输入、连续输出的信道。信道的输出是一个随机变量，它可以取到实数轴上的任一点的值，即 y\in \{-\infty,+\infty\} 。如果物理信道仅受到均值为0，单边谱密度是N_0 的加性白色高斯噪声的影响，则信道的输出是均值为0，方差为\sigma^2 = N_0/2 的高斯随机变量。在此情况下，我们得到了一个离散输入、连续输出的无记忆高斯信道。该信道特征可以由一组 M 个条件概率密度函数 p(y\mid x) 来完全刻画，其中 x\in\{0,1,\cdots,M-1\} 。对于M=2 和x\in\{0,1\} 的特殊情况，我们得到一个二进制输入、连续输出的无记忆高斯信道。如果采用BPSK调制，则信道特征可以由下列条件概率密度函数来完全描述：

p(y \mid x=0)=\frac{1}{\sqrt{\pi N_{0}}} \mathrm{e}^{-\frac{y+\sqrt{E_{s}}}{N_{0}}}, \quad p(y \mid x=1)=\frac{1}{\sqrt{\pi N_{0}}} \mathrm{e}^{-\frac{y-\sqrt{E_{s}}}{N_{0}}} \tag{*}

其中E_s 是信号能量。

若在给定时间间隔内检测器的输出不仅与当前间隔内的传输符号有关，而且与以前时间间隔的传输符号也有关，则该信道称为有记忆(memory) 的。衰落信道是有记忆信道的一个典型例子，这是由于多径传输破坏了间隔之间的独立性。对于有记忆信道，我们很难构造出合适的模型，而且在这样的信道上进行编码与其说是一门科学，还不如说是一门艺术。

4 最大似然译码

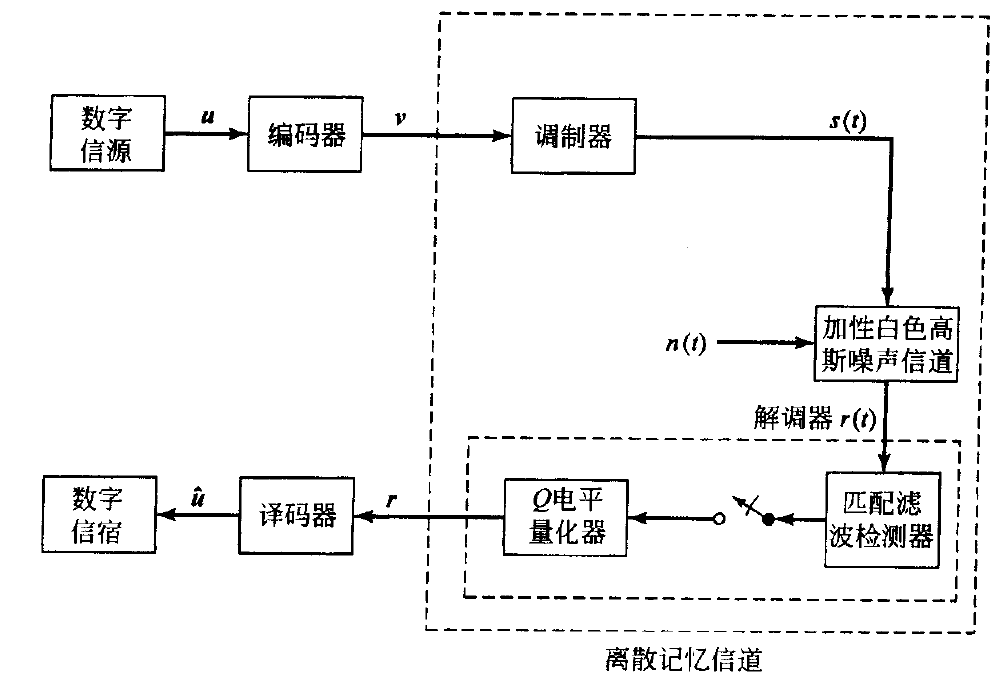
$Pasted image 20240305165327 | \mid 500|475$
上图给出了一个在AWGN信道上采用有限输出量化的编码系统框图。

在分组编码系统中，信源输出 \boldsymbol{u} 代表一个k 比特信息，编码器输出\boldsymbol{v} 代表一个 n 符号码字，解调器输出 \boldsymbol{r} 代表相应的 Q 进制的接收 n 维向量，译码器输出 \hat{\boldsymbol{u}} 代表编码消息的 k 比特估值。
在卷积编码系统中，\boldsymbol{u} 代表含 kh 个信息比特的序列，而 \boldsymbol{v} 代表一个含有 N \triangleq nh+nm = n(h+m) 个符号的码字，其中 kh 是信息序列的长度， N 是码字的长度。当最末的一个信息比特分组进入编码器后，由于编码器具有 m 个单元的存储器，这时将产生 nm 个附加的编码符号。解调器的输出\boldsymbol{r} 是一个 Q 进制的接收 N 维向量，译码器输出 \hat{\boldsymbol{u}} 是信息序列的一个 kh 比特估值。

译码器必须根据接收序列 \boldsymbol{r} 产生对信息序列 \boldsymbol{u} 的一个估值 \hat{\boldsymbol{u}} 。由于信息序列 \boldsymbol{u} 和码字 \boldsymbol{v} 之间有一一对应关系，这就等效于译码器能产生码字 \boldsymbol{v} 的一个估值 \hat{\boldsymbol{v}} 。显然，当且仅当 \hat{\boldsymbol{v}}=\boldsymbol{v} 时，\hat{\boldsymbol{u}}=\boldsymbol{u} 。译码规则 (decoding rule) 就是对每个可能的接收序列 \boldsymbol{r} 选择一个估值码字 \hat{\boldsymbol{v}} 的策略。若传递的码字是 \boldsymbol{v} ，当且仅当 \hat{\boldsymbol{v}}=\boldsymbol{v} 时出现译码错误 (decoding error)。若给定接收为 \boldsymbol{r} ，则译码器的条件误码率 (conditional error probability of the decoder) 定义为

P(E\mid \boldsymbol{r})\triangleq P(\hat{\boldsymbol{v}}\neq \boldsymbol{v}\mid \boldsymbol{r})

于是，译码器的误码率(error probability of the decoder)由

P(E)=\sum_{r} P(E \mid r) P(r)

给定，其中P(\boldsymbol{r})为接收序列为 \boldsymbol{r} 的概率。由于 \boldsymbol{r} 是在译码前产生的，故P(\boldsymbol{r}) 与所用的译码规则无关。因此，最优译码规则（即能使 P(E) 最小的规则）必须对所有 \boldsymbol{r} 使得 P(E\mid \boldsymbol{r})=P(\hat{\boldsymbol{v}} \neq \boldsymbol{v}\mid \boldsymbol{r})为最小。由于使P(\hat{\boldsymbol{v}} \neq \boldsymbol{v}\mid \boldsymbol{r}) 最小等价于使 P(\hat{\boldsymbol{v}} = \boldsymbol{v}\mid \boldsymbol{r}) 最大，因此对于给定的 \boldsymbol{r} , 选择使

P(\boldsymbol{v} \mid \boldsymbol{r})=\frac{P(\boldsymbol{r} \mid \boldsymbol{v}) P(\boldsymbol{v})}{P(\boldsymbol{r})} \tag{1}

为极大的\hat{\boldsymbol{v}} 作为码字 \boldsymbol{v} 可使得 P(E\mid \boldsymbol{r}) 最小；也就是说，在给定接收序列 \boldsymbol{r} 的情况下，要选择最大似然码字作为 \hat{\boldsymbol{v}} 。若所有的信息序列，进而所有的码字都是等概出现的，即 P(\boldsymbol{v}) 对于所有的 \boldsymbol{v} 都相同，则使公式（1）最大就等价于使 P(\boldsymbol{r}\mid \boldsymbol{v}) 最大。对于离散无记忆信道有

P(\boldsymbol{r} \mid \boldsymbol{v})=\prod_{i} P\left(r_{i} \mid v_{i}\right) \tag{2}

这是由于无记忆信道的每个接收符号只与相应的传输符号有关。选择其估值以使得公式（2）为最大的译码器称为最大似然译码器（maximum likelihood decoder, MLD） 。由于 \log x 是 x 的单调增函数，故最大化公式（2）等价于最大化对数似然函数

\log P(\boldsymbol{r} \mid \boldsymbol{v})=\sum_{i} \log P\left(r_{i} \mid v_{i}\right) \tag{3}

对离散无记忆信道，MLD选择能使公式（3）的和为最大的 \hat{\boldsymbol{v}} 作为码字 \boldsymbol{v} 。若码字不是等概的，由于在决定哪个码字能使 P(\boldsymbol{v} \mid \boldsymbol{r}) 最大的时候必须以码字概率 P(\boldsymbol{v}) 对条件概率 P(\boldsymbol{r} \mid \boldsymbol{v}) 进行加权，所以MLD不一定是最优的。然而在很多情况下，接收端并不能确切地知道码字概率，从而无法做到最优译码，此时MLD就成了可行的最优译码规则。

现在，考虑将MLD译码规则应用于BSC。在这种情况下，\boldsymbol{r} 是一个二进制序列，由于信道噪声的影响，它可能在某些位置上不同于发送码字 \boldsymbol{v} 。当r_{i} \neq v_{i} 时，P(r_{i} \mid v_{i})=p ；而当r_{i} = v_{i} 时，P(r_{i} \mid v_{i})=1-p 。令 d(\boldsymbol{r},\boldsymbol{v})表示\boldsymbol{r} 和\boldsymbol{v} 之间的距离，也就是\boldsymbol{r}和\boldsymbol{v} 不同的位置数。该距离被称为汉明距离(Hamming distance) 。对于长度为 n 的分组码，公式（3）可以变形为

\begin{aligned} \log P(\boldsymbol{r} \mid \boldsymbol{v}) & =d(\boldsymbol{r}, \boldsymbol{v}) \log p+[n-d(\boldsymbol{r}, \boldsymbol{v})] \log (1-p) \\ & =d(\boldsymbol{r}, \boldsymbol{v}) \log \frac{p}{1-p}+n \log (1-p) \end{aligned}\tag{4}

（对于卷积码，公式（4）中的 n 要用 N 代替）。由于p<\frac{1}{2} 时，\log \frac{p}{1-p}<0 ，且对所有\boldsymbol{v} ，n\log(1-p) 是一个常数，故BSC下的MLD译码规则就是选择能使得\boldsymbol{r} 和\boldsymbol{v} 之间距离d(\boldsymbol{r},\boldsymbol{v})为最小的\hat{\boldsymbol{v}} 作为码字\boldsymbol{v} ，即选择与接收序列不同的位置为最小的\boldsymbol{v} 作为码字。因此，BSC的MLD有时也叫做最小距离译码器(minimum distance decoder)。

对于离散输入、连续输出的无记忆信道，接收序列\boldsymbol{r} 是实数序列。为了计算条件概率P(\boldsymbol{r}\mid \boldsymbol{v}) ，我们简单地将公式（2）中的乘积中的每个符号转移概率 P(r_{i}\mid v_{i}) 替换为公式(*)给出的对应的条件概率密度函数。

有噪信道编码定理(noise channel coding theorem)和MLD的复杂度

有噪信道可靠传输信息的能力已经由香农在其独创性的论文中给出。这个结果称作有噪信道编码定理(noise channel coding theorem) ，它证明：每个信道都有一个信道容量 C ，对任意满足R<C的速率R ，都存在传输速率为R 的码，用最大似然译码可以达到任意小的译码误码率P(E) 。特别地，对于任意R<C ，存在着分组长度 n 足够大的分组码，使得

P(E)\leq 2^{-nE_{b}(R)} \tag{5}

同时，存在存储级数m 足够大的卷积码，使得

P(E)\leq 2^{-(m+1)E_{c}(R)} \tag{6}

对于R<C ，E_{b}(R)和E_{c}(R)为R 的正函数，且完全由信道特性决定。公式（5）给出的上界说明，对于任何固定的R<C ，分组编码可在保持比值k/n 为常数的同时，通过增加分组长度n 来获得任意低的误码率。公式（6）的上界说明，对于任何固定的R<C ，卷积编码可在保持k 和n 不变时通过增加存储级数m 来获得任意低的误码率。

有噪信道编码定理是建立在对随机编码(random coding) 的讨论基础上的。所得到的性能界实际上是全体码集合上的平均误码率。由于某些码的性能一定优于这个平均值，因此有噪信道编码定理保证了满足公式（5）和（6）的码的存在性，但并未指出如何去构造它们。进一步说，对于固定速率R<C的分组码，为了获得很低的误码率，需要较长的分组长度。这要求码字的数目2^k=2^{nR} 必然很大。由于MLD必须对每个码字计算\log P(\boldsymbol{r} \mid \boldsymbol{v}) ，然后选择给出最大值的码字，这使得MLD必须进行计算的次数随着n 的增加变得非常大。对于卷积码而言，低误码率要求高阶的存储级数。因此，采用最大似然译码来获得非常低的误码率是不切实际的。所以，在设计一个要实现低误码率的编码系统时会碰到下面两个主要的问题：

如何构造好的长码，在用最大似然译码时，它的性能要满足公式（5）和（6）；
寻求易于实现的编译码方法，使其实际性能接近最大似然译码所达到的性能。

5. *错误类型

随机错误信道(random error channels) - 一般是无记忆信道 -> 纠随机错误码（random-error correcting codes）- 常见的信道编码一般都是这种编码。
突发错误信道(burst error channels) - 一般是有记忆信道（衰落信道）-> 纠突发错误码 (burst-error correcting codes)
混合信道(compound channels) -> 纠突发和随机错误码(burst- and- random-error correcting codes)。

6. 差错控制策略

前向纠错（Forward error correction, FEC）：利用纠错码在接收端自动地纠出检出的错误。
自动请求重传（Automatic Repeat Request, ARQ）：当接收端检测出错误时，就向发送端发出要求重传该消息的请求，直到该消息被正确接收为止。
- 等待式（stop- and- wait）ARQ ：发送端发送一个码字给接收端，然后等待从接收端返回的一个肯定（ACK）或否定（NACK）的应答。若收到的是ACK，发送端就发送下一个码字；但是如果收到的是NACK，发送端就重新发送前一个码字。当噪声持续存在时，同一个码字在被正确接收和应答前，可能需要反复发送若干次。
- 连续式（continuous）ARQ ：发送端连续地将码字发送到接收端，同时连续地接收确认信号。
  - 当收到NACK时，发送端开始重传。发送端可以回退到发生错误的码字，并且重传该码字及其后续的N-1个码字，这称做退N步(go-back-N)ARQ。
  - 另一种可选的方案是发送端仅重发那些有否定应答的码字，这称为选择重传(selective-repeat) ARQ。
  - 选择重传ARQ比退N步ARQ更为有效，但是要求更复杂的逻辑和更大的缓存。
- 连续式ARQ比等待式ARQ的效率更高，但是实现的代价也更大。
  - 在卫星通信系统中，由于传输速率高且往返时延大，通常采用连续式ARQ。
  - 如果系统传输一个码字所花费的时间相较于收到一个应答的时间长，则一般采用等待式ARQ。
  - 等待式ARQ是为半双工信道设计的。
  - 连续式ARQ是为全双工信道设计的
ARQ相较于FEC的优劣势在于：
- 检错对译码设备的要求远比纠错简单。
- 从信息只在出现错误的时候才被重传的意义上来说，ARQ是一个自适应系统。
- 当信息的错误率较高时，重传必然过于频繁，此时系统吞吐量(system throughput)——正确接收新产生的消息的速率，将由于ARQ而降低。

混合（Hybrid）ARQ机制——结合了FEC和ARQ的优势

7. 性能的衡量

一个编码通信系统的性能通常用译码错误的概率（称为误码率（error probability） ）和相对于具有相同传输速率的非编码系统的编码增益（coding gain） 来衡量。

7.1 误码率

误码率分为两种不同类型

字的误码率定义为译码器输出的码字（或分组）有错误的概率，通常被称作为误字率（word-error rate, WER） 或误分组率（block-error rate, BLER） 。
比特的误码率定义为译码器输出的译码信息比特发生错误的概率，称为误比特率（Bit-error rate, BER） 。

在一个码率为 R=k/n的编码通信系统中，为传输每个信息比特需要传输符号（或信号）的数目为 1/R 。若每个传输符号的能量为E_{s} ，则每个信息比特对应的能量E_{b} 为

E_{b}=\frac{E_{s}}{R}

一个编码通信系统的误码率通常用单位信息比特的能量E_{b}与信道噪声的单边功率谱密度N_{0} 的比值的形式来表示，E_b/N_0 称为信噪比（signal-to-noise ratio, SNR） ，其单位通常用分贝（dB）来表示。

7.2 编码增益

编码系统的另一个性能衡量指标是编码增益。编码增益的定义如下：

为获得一个特定的误码率（BER或WER），编码系统所需的E_b/N_0比非编码系统的减少值。

获得额外编码增益的代价是更高的译码复杂度开销。在每分贝性能提高都将减少整个系统开销的通信应用中，编码增益相当重要。

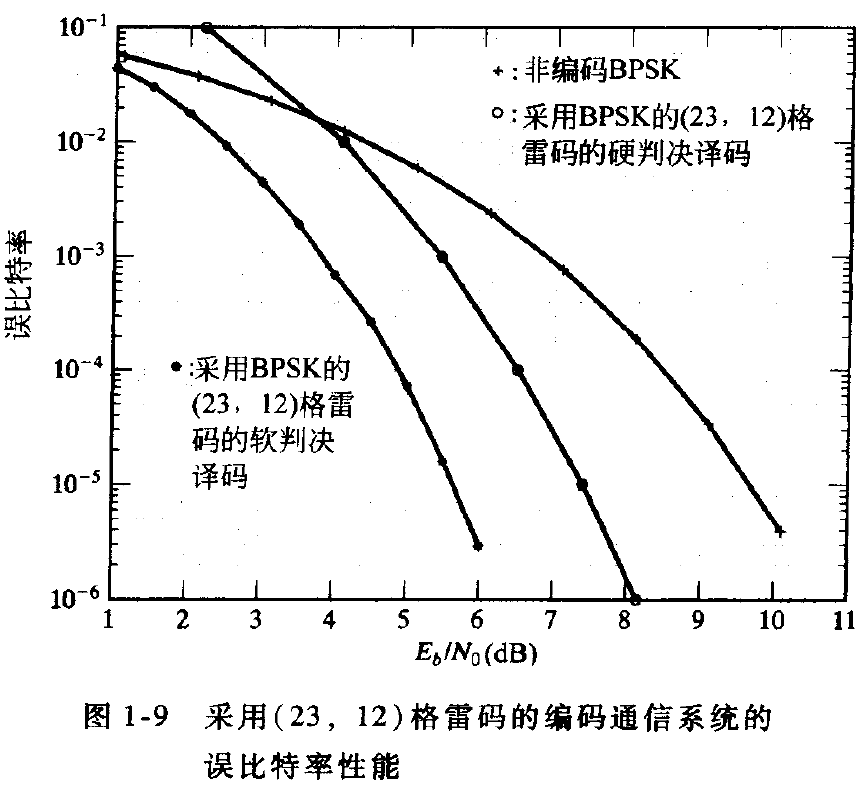
Pasted image 20240306094956

从上图中可以看出，在E_b/N_0 的值足够低时，编码增益的值变为负数。这个阈值现象对所有的编码方案都存在。总存在一个E_b/N_0 的值，当低于它时，编码将毫无效果，而且使情况变得更糟。这个SNR称为编码阈值（coding threshold）。让这个阈值足够地并且保证编码通信系统工作在SNR远高于编码阈值的状态相当重要。

上图中，

当BER=10^{-5} 时，硬判决格雷码比非编码BPSK系统有2.15dB的编码增益，而软判决译码（MLD）则获得了超过4.0dB的编码增益。
硬判决格雷码的编码阈值为3.7dB。

渐进编码增益（asymptotic coding）——高SNR下的编码增益

渐进编码增益只与码率 R 和码的最小距离 d_{\min} 有关，其中 d_{\min} 定义为任意两个码字之间的最小汉明距离。在高SNR的条件下，采用相干检测的非编码BPSK的误比特率

p=Q\left(\sqrt{2 E_{s} / N_{0}}\right)

可将Q函数近似为Q(x)\leq \frac{1}{2}e^{-x^2/2}, x\geq0 ，于是得到

\left(P_{b}\right)_{\text {uncoded }} \approx 1 / 2 \mathrm{e}^{-\left(E_{b} / N_{0}\right)_{\text {uncoded }}} \tag{7}

在高SNR条件下，采用软判决（未量化的）MLD，具有最小距离d_{\min} 的(n,k) 分组码的误比特率可近似为（后面补充推导）：

\left(P_{b}\right)_{\text {coded }} \cong K \mathrm{e}^{-d_{\min } R\left(E_{b} / N_{0}\right)_{\text {coded }}}\tag{8}

其中R=k/n 为码率，且K 是一个通常较小的仅与码相关的常数。令公式（7）和（8）相等可以计算出SNR的降低值，具体为

K \mathrm{e}^{-d_{\min } R\left(E_{b} / N_{0}\right)_{\text {coded }}}=\frac{1}{2} \mathrm{e}^{-\left(E_{b} / N_{0}\right)_{\text {uncoded }}}\tag{9}

两边取自然对数，注意到当E_b/N_0 较大时\log K 和\log \frac{1}{2} 可以忽略，我们得到

\frac{\left(E_{b} / N_{0}\right)_{\text {uncoded }}}{\left(E_{b} / N_{0}\right)_{\text {coded }}}=R d_{\text {min }}\tag{10}

因此，具有最小距离d_{\min} 的(n,k)码采用软判决MLD时相对于非编码BPSK的渐进编码增益由下式给出：

\gamma_{\text {asymp }}=10 \log _{10} R d_{\min }\tag{11}

对于硬判决MLD，证明了渐进编码增益为

\gamma_{\text {asymp }}=10 \log _{10} \left( \frac{1}{2} \right)R d_{\min }\tag{12}

可以看出，软判决MLD比硬判决MLD多出3dB的渐进编码增益。 只是在很大的SNR条件下，才能获得这3dB的编码增益，对于更为实际的SNR取值，软判决译码比硬判决译码的编码增益要小于3dB，一般介于2-2.5dB之间。

香农限

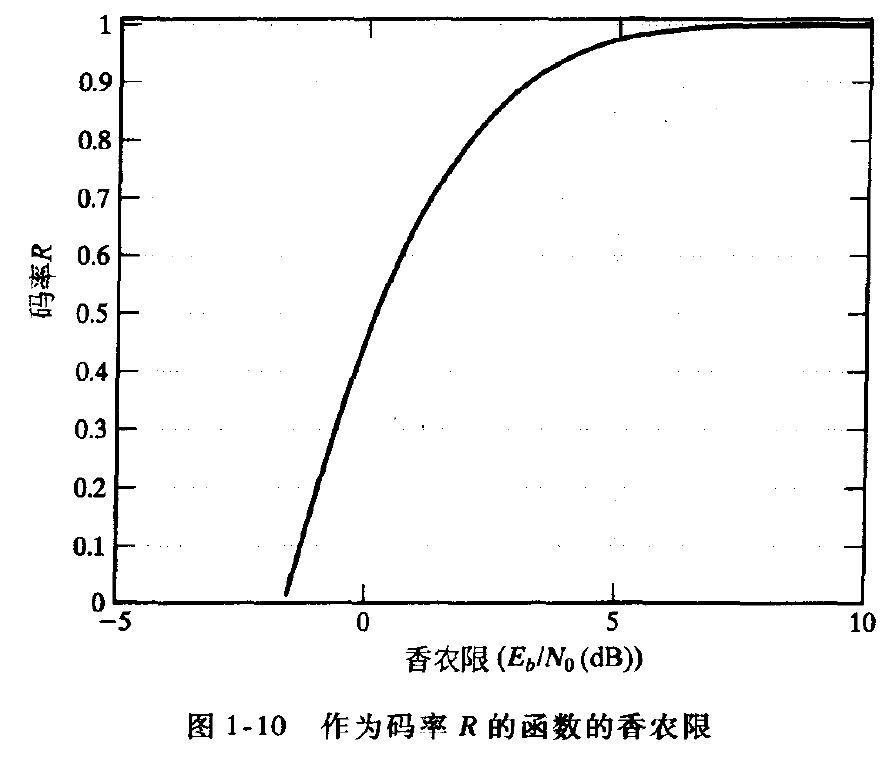
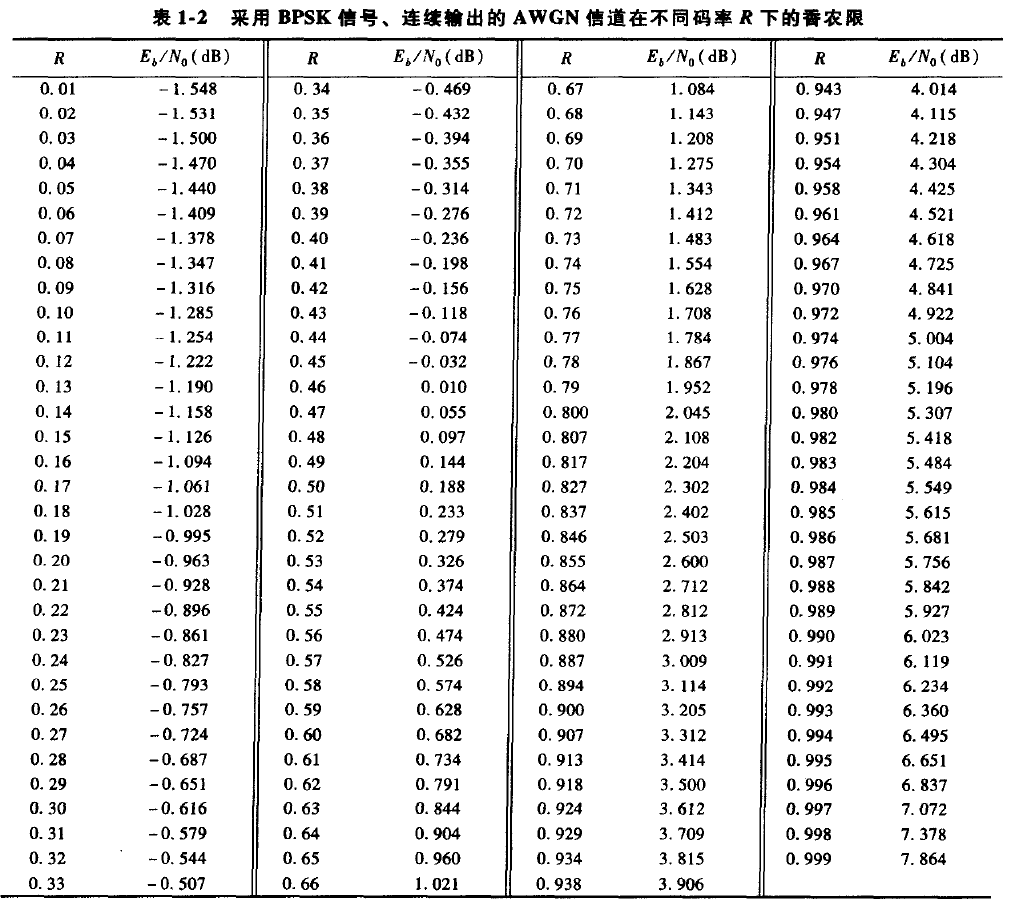
在为差错控制而设计编码通信系统时，总是希望获得特定误码率所需的 SNR 值尽量小。这与最大化编码系统相对于使用相同调制信号集的非编码系统所获得的编码增益等价。根据香农的有噪信道编码定理，可以推导出一个码率为R 的编码通信系统达到无误码传输状态(或任意小的误码率)所必须的最小SNR 的理论极限。这个理论极限通常称为香农限(Shannon limit)，它说明对一个码率为R 的编码通信系统，只有当SNR超过这个极限值时才可能获得无误码传输。只要 SNR 高于这个极限值，香农的编码定理保证了能够获得无误码传输的(可能相当复杂)编码通信系统的存在性。对采用 BPSK 信号的二进制输人、连续输出的AWGN信道上的传输，香农限(用E_b/N_0表示)作为码率 R 的函数没有显式表达，但是它可以用数值的方法进行计算。
Pasted image 20240306110416
Pasted image 20240306110435

目录CONTENT

差错控制编码学习笔记1：基础知识